Sampling Methoden: Sequentielles Sampling oder Monte-Carlo?

“Prognosen sind schwierig, insbesondere wenn sie die Zukunft betreffen”. Kein Zitat beschreibt die grundsätzliche Herausforderung des FI-Simulators besser als Dieses. Mangels Glaskugel basiert dieser Simulator daher auf der mehr oder weniger intelligenten Generierung von möglichen Kursentwicklungen in der Zukunft und der Analyse der Verteilung einer größeren Menge solcher generierter Kursentwicklungen. Dieser Artikel beschreibt die Details der Generierung und vergleicht die Vor- und Nachteile der unterschiedlichen Methoden.

1. Sequentielles Sampling

Sequentielles Sampling (auch wenn es bislang nicht explizit so bezeichnet war) war bis zur Version 0.7 das einzige Sampling-Verfahren, das im Simulator verfügbar war. Wie bereits im Grundlagenartikel beschrieben, entspricht dann jeder Startmonat unserer historischen Kursdaten einer möglichen zukünftigen Entwicklung unseres Portfolios, einfach indem wir die komplette, auf diesen Startmonat folgende, historische Kursentwicklung aller Assets noch einmal auf das heutige Portfolio anwenden. Nutzt man die am weitestesten zurück reichenden Datenreihen, z.B. die Shiller Daten des US Aktienmarkts (ab Anfang 1871) oder die Gielen Daten des deutschen Aktienmarkts (ab Ende 1869) erhält man daraus ca. 154 Jahre oder 1844 unterschiedliche Startmonate, die ein gewisses Spektrum möglicher zukünftiger Kursentwicklungen aufspannen.

Vorteil dieser Methode ist, neben der einfachen Umsetzung, auch die bestmögliche Bewahrung zeitlicher Korrelationen. D.h. falls Märkte nach irrationalen Übertreibungen nach oben oder unten wieder zurück zu ihrem langjährigen Mittelwert streben würde dies automatisch eben auch in unseren zukünftigen Kursentwicklungen berücksichtigt.

Nachteile dieses Verfahrens sind neben der grundsätzlichen statistischen Begrenzung auf die verfügbaren Startmonate aber auch eine hohe Korrelation der damit erzeugten Varianten. Eine Kurshistorie die im Sept. 1929 startet unterscheidet sich natürlich nur marginal von derjenigen, die im Okt. 1929 startet. Beide haben die komplette Weltwirtschaftskrise noch vor sich und die damit erzielbaren Entnahmeraten sind sehr ähnlich. Dies sieht man auch sehr schön, wenn man sich die Entnahmeraten in Abhängigkeit vom Startmonat anschaut. Die Entwicklung der Entnahmeraten je Startmonat folgt einer stetigen Kurve:

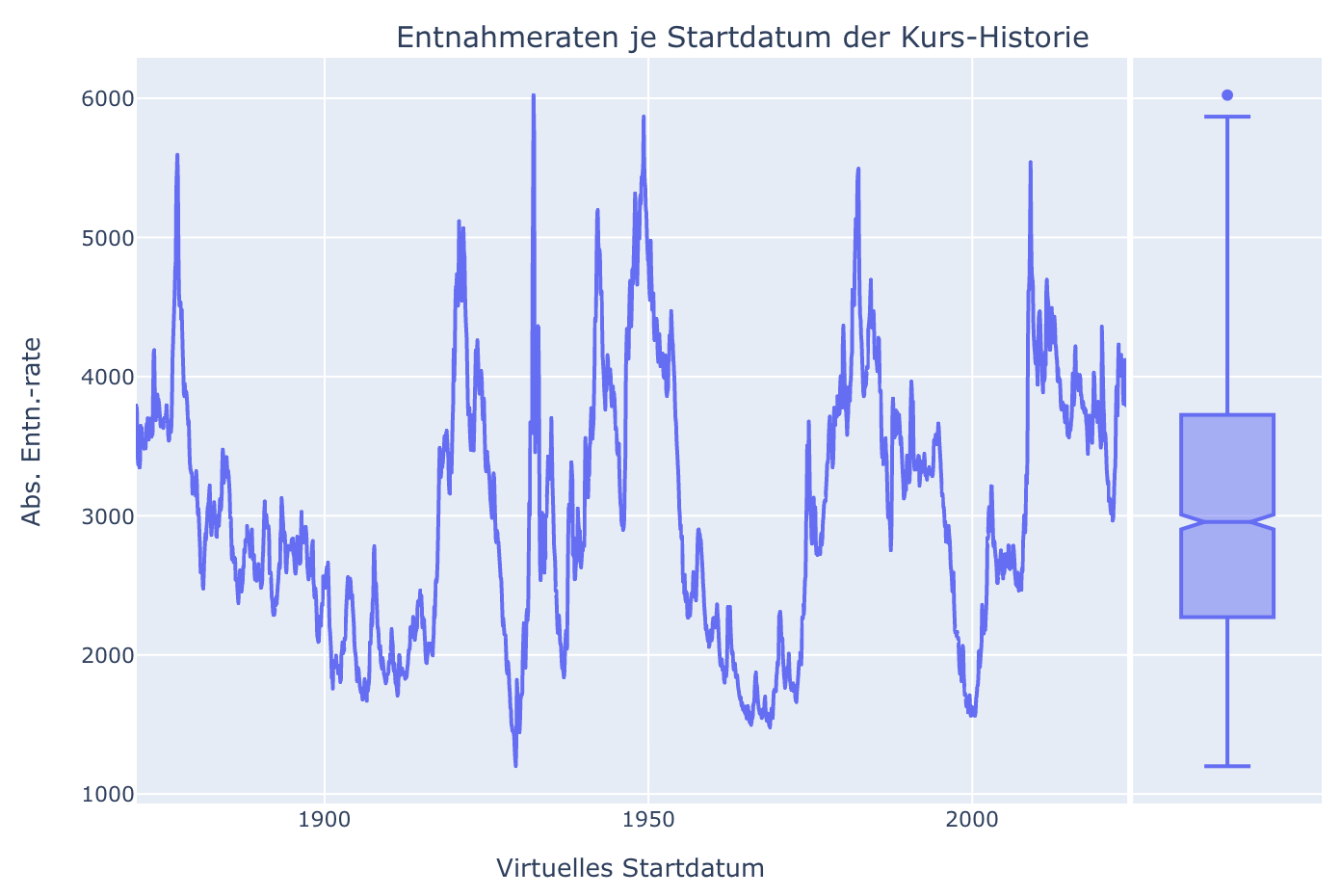
Dies erleichtert zwar die inhaltliche Analyse des Rendite-Reihenfolge-Risikos zeigt aber ganz deutlich, wie ähnlich die Datenpunkte eigentlich einander sind. Statistisch haben wir hier sicherlich keine 1800 unabhängigen Messpunkte vorliegen. Darüberhinaus ist die Historie, die unsere Kursdaten abdeckt naturgemäß begrenzt. Ja, Daten ab 1871 beinhalten sicherlich zwei Weltkriege, verschiedene Wirtschaftskrisen und mehrere Zinszyklen und unsere Grundannahme, dass die zukünftige Kursentwicklung vermutlich zwischen den damit aufgespannten Extremen liegt, ist sicher auch nicht völlig abwegig (Nicht umsonst ist dieses Verfahren eines der Quasi-Standards). Dennoch bleibt hier aufgrund der geringen Statistik immer ein ungutes Bauchgefühl zurück. Wie heisst es so schön: Woran erkennt man, dass Wirtschaftswissenschaftler Humor haben? Sie verwenden Dezimalpunkte. Ein Blick auf meine Tabelle zur exakten Berechnung von Entnahmeraten mit Dezimalpunkt und sogar zwei Dezimalstellen zeigt schon, dass ich mindestens genau so viel Humor habe.

Ab der Version 0.7 gibt es daher alternative Möglichkeiten im Simulator, solche Historien zu generieren. Diese beruhen auf Monte-Carlo Simulationen und adressieren einige dieser berechtigten Kritikpunkte.

Problem: Korrelationen zwischen unterschiedlichen Assets

Die einfachste Möglichkeit neue Kursreihen zu erzeugen, wäre monatliche Renditen mit einem simplen Zufallszahlengenerator zu ermitteln und aneinander zu reihen. Typischerweise würde man Renditen erzeugen, die um den historisch bekannten Mittelwert schwanken und die Schwankungsbreite ebenfalls den historischen Schwankungen anpassen (Eine völlig willkürliche Festlegung von Mittelwert und Schwankungsbreite würde den daraus entstehenden Entnahmeraten jegliche Vorhersagekraft rauben). Dieser Ansatz hat in einer Multi-Asset Simulation wie unserer aber trotzdem einen gravierenden Nachteil: Auch wenn wir fein säuberlich die historischen mittleren Renditen und Varianzen für jedes bekannte Asset ermitteln und in die Simulation einsetzen, würden wir damit ein fundamental wichtiges Phänomen komplett ignorieren: Die Renditen unterschiedlicher Assets waren historisch immer miteinander korreliert! Z.B. haben in Krisen oft Staatsanleihen an Wert gewonnenen, während Aktienkurse auf Tauchfahrt gegangen sind. Dies ist ja letztlich der Hauptgrund warum Berater eine Beimischung von Anleihen empfehlen und warum wir uns überhaupt so viele Gedanken über unsere eigene Asset-Allokation machen. Einfache Monte-Carlo Simulationen würden solche Korrelationen zwischen unterschiedlichen Assets aber komplett ignorieren und wären daher für solche Untersuchungen schlicht unbrauchbar.

Eine mögliche Gegenmaßnahme wäre, die historischen Korrelationen ebenfalls zu ermitteln und den Zufallszahlengenerator entsprechend zu instruieren, nur noch solche passend korrelierten Zufallsrenditen auszuspucken. Dieser Ansatz wird letztlich dadurch begrenzt, dass solche Korrelationen historisch leider auch nie konstant waren. Versucht man aber auch die zeitliche Entwicklung dieser Korrelationen zu berücksichtigen leidet die Genauigkeit der Berechnungen an der begrenzten historischen Datenmenge. D.h. man füttert letztlich zunehmend immer unsicher berechnete Parameter in eine zunehmend komplexere Simulation ein. Es gibt aber zum Glück etwas abgewandelte Monte-Carlo Ansätze, die einfach genug sind und diesem Problem Rechnung tragen.

2. Monte Carlo mit IID Renditen

Ein einfacher Ausweg aus dem oben beschriebenen Dilemma, die wichtigen Korrelationen zwischen Assets in einer Monte Carlo Simulation zu bewahren läuft unter der Abkürzung IID und steht für “Independent and identically distributed Returns”. In diesem Verfahren werden keine neuen Renditen zufällig generiert sondern es werden historische Renditen zufällig ausgewählt und zwar zeitlich unabhängig voneinander und gleichverteilt. D.h. angenommen wir benötigen zufällige Kursentwicklungen für 30 Jahre, also 360 Monate, dann würden wir für eine neue, zufällige Zeitreihe aus den existierenden gut 1800 historischen Renditen, 360 Zufällige auswählen und aneinander reihen. Und ganz wichtig: Um die Korrelationen zwischen unterschiedlichen Assets zu erhalten würde hier jedes Asset die passende Rendite aus dem gleichen Ursprungsmonat erhalten.

Eine solche Simulation ist einfach zu implementieren und seit der Version 0.7 im FI Simulator auswählbar. Dazu öffnet man den Reiter “Einstellungen Asset Allokation, Kurs- und Inflationsdaten” und wählt im neuen Feld “Sampling Verfahren” einfach “IID” aus:

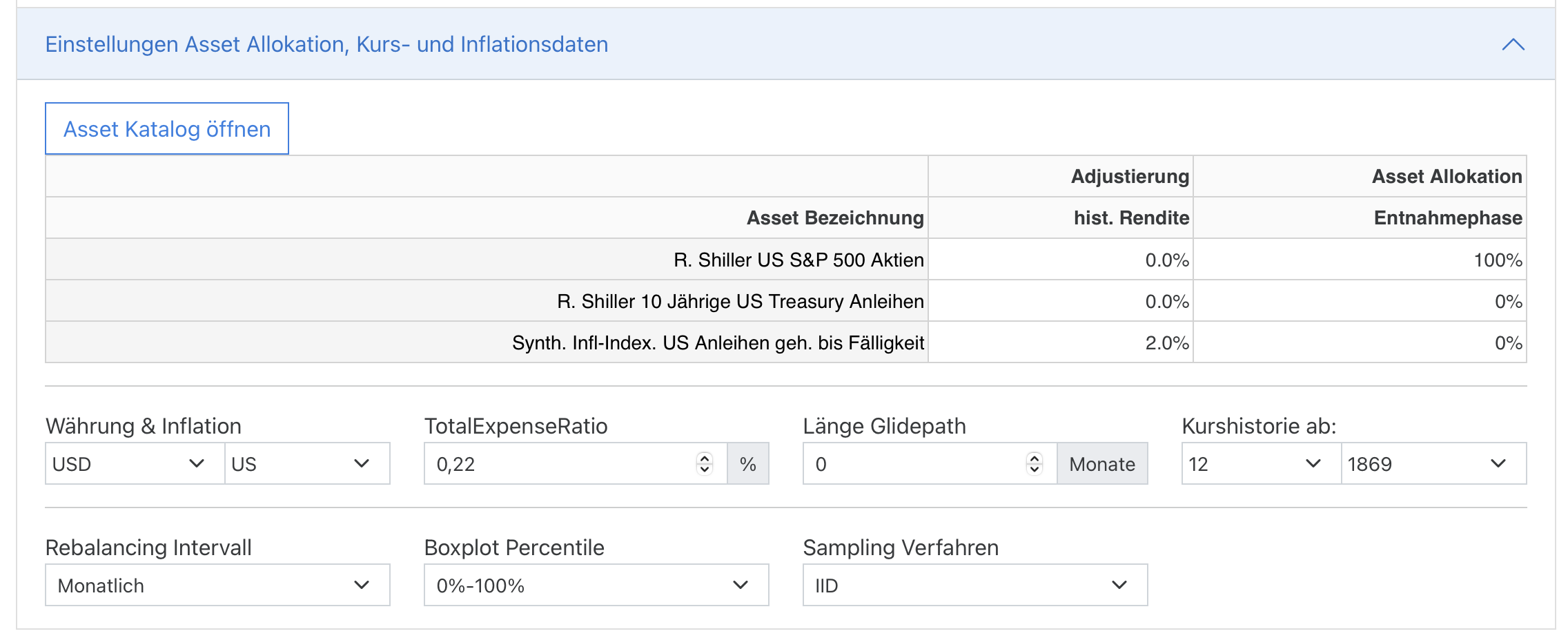
Schaut man sich dann die berechneten Entnahmeraten an, sieht man ein deutlich anderes Bild als oben:

In unserem Simulator erzeugen wir bei den Monte-Carlo Verfahren jeweils 5000 zufällige Kursentwicklungen, die jeweils einem Punkt entsprechen. Diese Punkte sind jetzt nur der Übersichtlichkeit halber auf der horizontalen Achse verteilt und entsprechen nicht mehr wie oben einem historischen Startmonat. Schaut man sich die vertikale Achse an, fällt zunächst auf, dass die Bandbreite der möglichen Entnahmeraten gestiegen ist. Offenbar enthält eine zufällig mit IID-Renditen gefüllte Auswahl von Zeitreihen noch deutlich extremere Fälle als unsere einfache sequentielle Simulation, die sich nur im Startmonat unterscheidet. Die “sichere” Entnahmerate im hier dargestellten einfachen Trinity-Fall mit 480.000 Euro Startportfolio und 30 Jahren Entnahme beträgt jetzt nur noch kümmerliche 737 EUR statt der “gewohnten” 1200 EUR mit sequentiellem Sampling. Auf der anderen Seite könnten wir bei optimaler Kursentwicklung jetzt aber über 9500 EUR pro Monat entnehmen gegenüber “nur” 6000 EUR mit sequentiellem Sampling.

Diese Extremwerte sind darüberhinaus jetzt auch nicht mehr exakt reproduzierbar. Ein Refresh des Browser-Fensters führt dazu, dass wieder 5000 neue zufällige Kursreihen gebildet werden und diese werden abweichende Minimal- und Maximalwerte zeigen. Teilweise können diese Abweichungen sogar extrem groß sein und es ist ganz hilfreich, sich dieses Verhalten einfach einmal durch mehrmaliges Refreshen anzusehen. Alle, die bislang im Simulator mit “sicheren” Entnahmeraten gerechnet haben, also genau den minimalen Werten mit angeblicher “0% Pleite-Gefahr”, dürften von diesem Verhalten nicht begeistert sein. Ich habe aber ganz bewusst, den sogenannten “Seed” des Zufallszahlengenerators hier nicht gespeichert. Damit könnte ich erreichen, dass bei jedem Aufruf immer dieselbe Zufallssequenz erzeugt wird und die Daten somit reproduzierbar wären. Dies würde aber genau dieses Phänomen unterdrücken und es ist aus meiner Sicht fundamental wichtig sich diese Zufälligkeit der Verteilung einmal bewusst zu machen. Die zukünftige Kursentwicklung ist schließlich ebenfalls nicht vorhersehbar und die bisherige exakte Reproduzierbarkeit der Ergebnisse schlicht eine Illusion, bzw. ein Artefakt des sequentiellen Samplings.

Aber es gibt trotzdem Hoffnung: Schauen wir uns dazu nicht die Extreme sondern den Median der Verteilung an, dieser liegt bei ca. 2960 EUR und schwankt auch nach Refresh des Browsers nur wenig. Dies liegt natürlich daran, dass Minimum und Maximum durch einzelne zufällig schlechte bzw. zufällig gute Kursentwicklungen definiert werden, während der Median eher die Gesamtheit der Kursentwicklungen wiederspiegelt. Der Median entspricht zwar der wahrscheinlichsten Entnahmerate, die aus unserem Portfolio realisiert werden kann, aber natürlich interessieren uns eher die schlechten Kursentwicklungen, da wir ja die damit verbundenden Risiken verstehen und deren Auswirkungen möglichst minimieren möchten. Wie können wir dies mit den neuen Monte-Carlo Verfahren jetzt tun?

Perzentile einschränken

Zu diesem Zweck existiert seit Version 0.7 jetzt im gleichen Reiter das ebenfalls neue Feld “Boxplot Perzentile”, das standardmäßig auf 0%-100% eingestellt ist. Dieses Feld ermöglicht es jetzt, die extremsten zufälligen Kursentwicklungen wieder auszublenden. Dazu setzen wir die Boxplot Perzentile einmal auf den Wert “1%-99%”, d.h. wir blenden damit die schlechtesten 1% und besten 1% aller zufälligen Kursentwicklungen aus. Die Untergrenze des Boxplots rechts verschiebt sich damit auf ca. 1190 EUR nach oben und bleibt nach Refresh auch wieder relativ konstant. Alleine durch Ausblenden von 2 mal 1% der extremsten Kursentwicklungen scheinen wir somit den Zufall wieder gebändigt zu haben.

Aber welchen Perzentilen sollte man bei den Monte-Carlo Simulationen nun also vertrauen? Diese Frage ist sehr grundsätzlicher Natur, nicht wirklich einfach zu beantworten und ich werde mich daher vor einer expliziten Antwort auch schlicht drücken. Ich würde aber die folgenden beiden Aspekte in den Raum werfen: Für eine relativ niedrige Schwelle spricht, dass extreme Kursentwicklungen schlichtweg zukünftig passieren können und eine konservative Risikoabschätzung sollte dem Rechnung tragen. Für eine eher hohe Schwelle spricht eine Überlegung, die ich bei William Bernstein einmal gelesen habe: Ein Blick zurück in die Geschichte würde die Wahrscheinlichkeit, in unserer Lebenszeit persönlich von einem Krieg betroffen zu sein, vermutlich in der Größenordnung von um die 10% ansiedeln. Macht es dann tatsächlich Sinn, schlechte Kursentwicklungen, die mit einer deutlich geringeren Wahrscheinlichkeit eintreten, in einer finanziellen Simulation zu berücksichtigen, wenn ein solcher Krieg noch ganz andere persönliche Risiken mit sich bringen würde?

3. Monte Carlo mit dem Stationary Block Bootstrap (SBB) Verfahren

Wir haben gesehen, dass Monte-Carlo Simulationen mit IID-Renditen gegenüber simplen Monte-Carlo Verfahren den Vorteil haben, Korrelationen zwischen unterschiedlichen Assets zu bewahren. Zeitliche Korrelationen innerhalb eines Assets gehen allerdings durch die Bedingung “Independent and identically distributed” komplett verloren. Um auch solche zeitlichen Korrelationen bei der zufälligen Generierung von Kursentwicklungen zu berücksichtigen müssen wir unser Verfahren noch etwas aufbohren. Der dafür notwendige Algorithmus wird als “Block Bootstrap Verfahren” bezeichnet und wurde 1994 von Dimitris Politis und Joseph Romano vorgestellt. Etwas vereinfacht wird in diesem Verfahren eine zufällige Kursentwicklung wie folgt aus der historischen Zeitreihe generiert:

Zunächst wird eine mittlere Blocklänge festgelegt, mit der alle Kursenwicklungen generiert werden sollen. Am Start wird ein zufälliger Startmonat aus der Historie ausgewählt und allen Assets die damaligen Renditen zugewiesen. Mit einer Wahrscheinlichkeit von (1-1/Blocklänge) wird dann am nächsten Monat auch genau der folgende Monat der Historie ausgewählt. An einem gewissen Punkt der Zeitreihe startet (mit Wahrscheinlichkeit 1/Blocklänge) aber wieder ein neuer Block, der dann auch wieder an einem zufälligen Startmonat der Historie beginnt. Im Endergebnis ist die zufällige, neue Kurshistorie dann aus einer Vielzahl von historischen Kursblöcken unterschiedlicher Länge zusammengesetzt, deren mittlere Länge aber genau der oben festgelegten Blocklänge entspricht. D.h. zeitliche Korrelationen bis etwa zu dieser Blocklänge bleiben in den neu generierten Kursreihen erhalten.

Dieses Verfahren ist jetzt ebenfalls im Feld “Sampling Verfahren” als “Block Bootstrap (SBB)” auswählbar. In diesem Fall erscheint dann auch ein zusätzliches Eingabefeld daneben, in dem die Blocklänge eingestellt werden kann:

Im Standard ist diese Blocklänge auf 120 Monate, also 10 Jahre eingestellt, d.h. die zufälligen Kursentwicklungen werden dann aus historischen Blöcken zusammengesetzt, die im Mittel 10 Jahre lang sind.

Schaut man sich die berechneten Entnahmeraten für das Standard Trinity-Beispiel an, erkennt man auf den ersten Blick wenig Unterschiede zur IID-Simulation (Die Perzentile wurden hier bei 1%-99% belassen, d.h. die Balken der Boxplots decken auch nur diesen Bereich der Punkte ab):

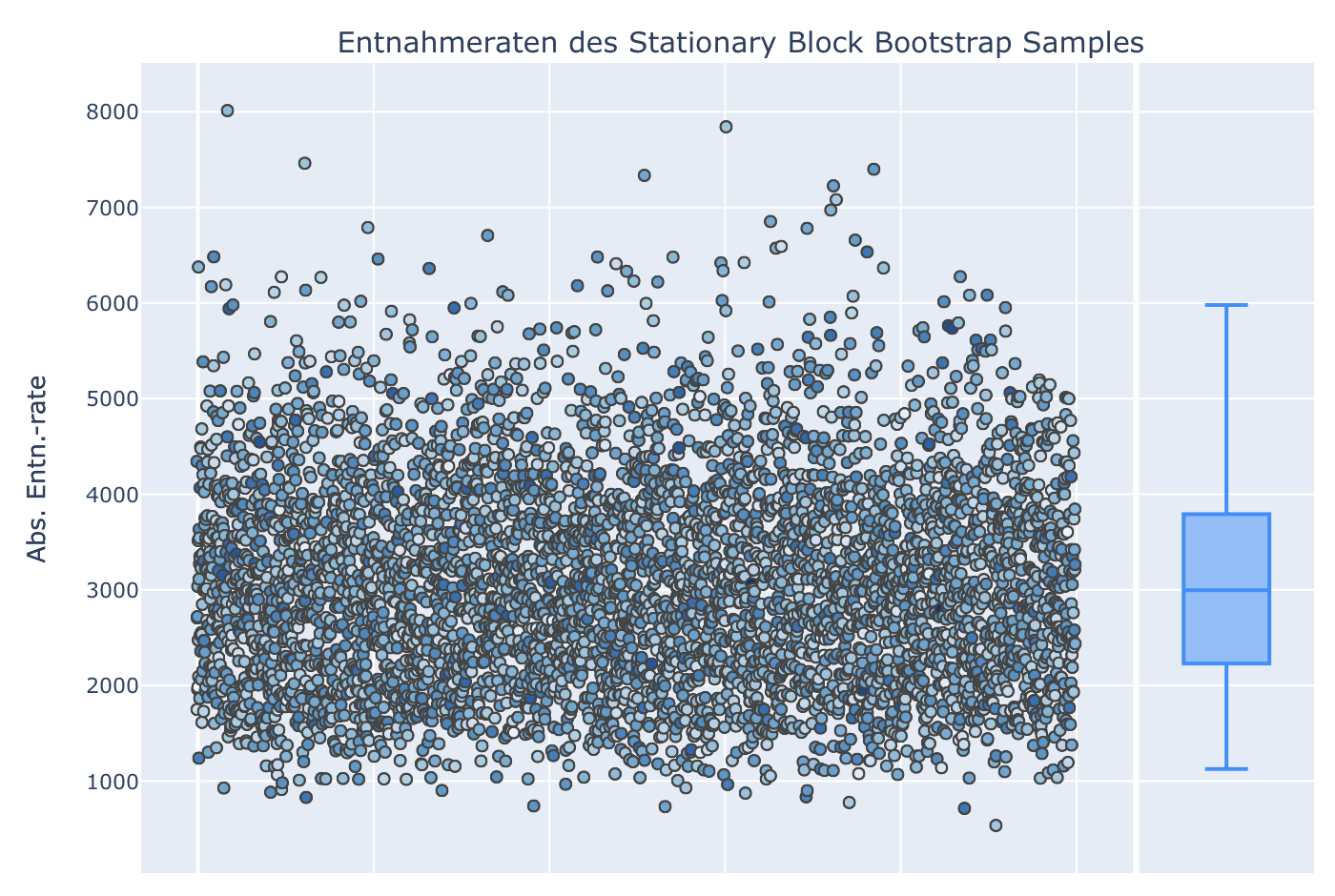
4. Vergleich der unterschiedlichen Sampling-Verfahren

Auch wenn die Ergebnisse des Block-Bootstrap Verfahrens auf den ersten Blick kaum von den Ergebnissen des Monte-Carlo mit IID Renditen unterscheidbar sind, lohnt sich ein genauerer Vergleich der Verfahren. Dazu betrachten wir zunächst die beiden möglichen Grenzfälle des Block-Bootstrap Verfahrens:

Gemäß der obigen Definition entspricht ein Block-Bootstrap mit Blocklänge 1 exakt der Monte-Carlo Simulation mit IID Renditen, d.h. IID ist der Grenzfall von Block-Bootstrap wenn die zeitlichen Korrelationen aufgrund der Blocklänge von 1 komplett verworfen werden.

Umgekehrt entspricht ein Block-Bootstrap mit unendlicher Blocklänge genau unserer bisherigen sequentiellen Simulation. D.h. wir sollten eigentlich feststellen, dass mit steigender Blocklänge die Unterschiede der Ergebnisse entsprechend kleiner werden.

Ab Version 0.7 ist ein solcher Vergleich der Sampling Verfahren als Unterreiter “Vergleich Sampling Verfahren” unterhalb des Reiters “Exakt berechnete Entnahmeraten” direkt auf Knopdruck verfügbar. Wichtig: Dieser Vergleich ignoriert dann natürlich das voreingestellte Sampling Verfahren und die Blocklänge, da er alle verfügbaren Verfahren und eine Auswahl von Blocklängen nebeneinander darstellt:

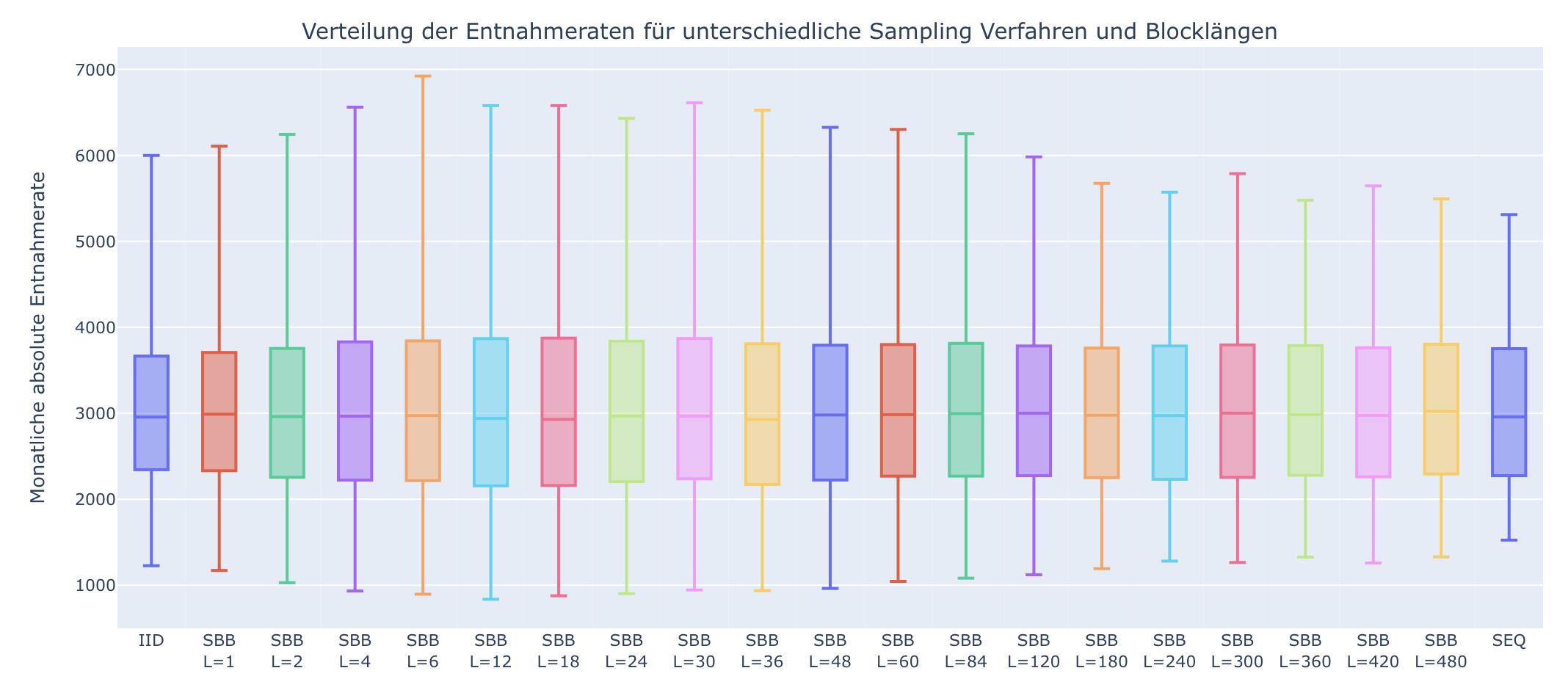
Nach der obigen Betrachtung dürfte es auch nicht verwundern, dass ganz links IID neben SBB mit Blocklänge L=1 dargestellt ist. Beide Verfahren sollten (im Rahmen der Statistik) identische Ergebnisse produzieren. Im Weiteren Verlauf wird dann die Blocklänge schrittweise vergrößert und man erkennt, dass die Bandbreite der Ergebnisse bis zu einer Blocklänge von ca. 20-30 erst ansteigt und danach wieder absinkt. Bei größeren Blocklängen nähert sich die Bandbreite der Ergebnisse wie erwartet dem bisherigen sequentiellen Sampling wieder an, welches ganz rechts zu finden ist.

Inhaltlich könnte es zunächst überraschen, dass offenbar ein Block-Bootstrap mit Blocklänge um die 25 noch “extremere Extreme” generiert als das IID Verfahren. Wenn man sich aber vor Augen führt, dass die echte Kursentwicklung der Börse eben keine reine Zufallsentwicklung ist, sondern immer auch von der Marktstimmung beeinflusst ist macht dieses Verhalten Sinn: Es gibt eben Marktphasen in denen aufgrund grenzenloser Euphorie eine Rekordrendite die nächste jagd und genau so gibt es Phasen, in denen die Frustration zu immer heftigeren Kurseinbrüchen führt. Solche emotionalen Übertreibungen behält der Block-Bootstrap dann bei und wenn dieses Verfahren, dann viele solcher extremen Euphorie- und Frustphasen zufällig aneinander reiht, dann sollte klar sein, dass die resultierenden Kursentwicklungen deutlich “extremere Extreme” enthalten sollten, als eine rein zufällig gemäß IID gewürfelte Verteilung.

Last but not least erkennt man, dass der Median der Verteilungen aber nahezu völlig unbeinflusst von der Wahl des Sampling Verfahrens bleibt.

5. Fazit

Die Hereinnahme von Monte Carlo Simulationen in den FI Simulator könnte einige Fragen aufwerfen, nicht zuletzt weil die neuen Verfahren die vielleicht liebgewonnene Präzision bei der Berechnung von Entnahmeraten vermissen lassen. Stabile Ergebnisse erfordern damit eine willkürliche Festlegung, welche Percentile in der Verteilung noch akzeptabel sind und welche lieber verworfen werden sollen. Ich kann mir vorstellen, dass einige damit unglücklich sind, allerdings empfinde ich diese Vorgehensweise als ehrlicher, weil sie letztlich transparent macht a) wie hoch die Unsicherheit in unseren Ergebnissen tatsächlich noch ist und b) wie subjektiv wir zwangsläufig auch bei der Interpretation von Ergebnissen sein müssen. In diesem Sinne hat die bisherige sequentielle Fortschreibung von historischen Daten, die sich nur im Startmonat unterscheiden aus meiner Sicht lediglich eine Scheinpräzision suggeriert, die in Wahrheit so nicht existiert. Monte-Carlo Verfahren mit ihrer inhärenten Zufallskomponte machen die Grenzen unserer Vorhersagekraft daher viel deutlicher und eignen sich somit für eine realistische Risikoanalyse vermutlich sogar besser.