Das Konzept hinter dem Simulator

Ausgangspunkt vieler Überlegungen zur finanziellen Freiheit ist die sog. Trinity Studie (englisch) aus dem Jahr 1998. Diese Studie besagt, dass jemand, der sich mit einem breit gestreuten Aktienportfolio zur Ruhe setzen möchte, trotz Kursschwankungen jährlich zwischen 3% und 4% dieses Portfolios entnehmen kann, ohne substantiell Gefahr zu laufen, dabei pleite zu gehen. Extrem verkürzt ist daraus die bekannte “4%-Regel” geworden, die die meisten aus dem FI-Umfeld bereits kennen werden.

Die Trinity-Studie im Simulator umgesetzt

Um das Konzept hinter dem Simulator besser zu verstehen, werden wir die Trinity-Studie zum Einstieg einmal nachbilden. Um das Beispiel parallel zum Lesen direkt nachzuvollziehen empfehle ich daher, den Simulator parallel in einem neuen Browser-Tab zu öffnen. Praktischerweise startet der Simulator standardmäßig fast genau mit den Eingangsdaten der Studie: Wir nehmen an, dass der aktuelle Wert unseres Aktienportfolios 480.000€ beträgt und möchten damit jetzt in den Ruhestand gehen. Gemäß der 4%-Regel dürften wir daher jährlich 19.200€, also monatlich 1.600€, aus diesem Portfolio durch Verkauf entsprechender Anteile entnehmen. Wir ignorieren an dieser Stelle erst einmal, dass wir beim Verkauf in der Regel noch eine Kapitalertragssteuer entrichten müssen und stellen fest, dass die 1.600€ bereits entsprechend im Feld “Ausgaben ab FI” eingetragen sind. Den Simulationszeitraum belassen wir in dem Beispiel bei 30 Jahren. Wären wir 60 Jahre alt und planen, einen Zeitraum bis zu unserem 90. Geburtstag abzudecken, wäre dies ein guter Wert. Den Start der Simulation sowie den FI-Zeitpunkt belassen wir beim aktuellen Monat, da wir ja einen Ruhestand zum jetzigen Zeitpunkt simulieren möchten.

Alle bekannten historischen Kursverläufe werden durchgespielt

Das schlimmste was dem angehenden Ruheständler jetzt passieren kann, ist das genau beim Beginn der regelmäßigen Entnahmen aus dem Depot ein Crash des Aktienmarkts passiert. Die monatlichen Entnahmen von 1.600€ erforden dann aufgrund des Kursverlustes plötzlich den Verkauf größerer Anteile, sodass das Depot sehr schnell abschmilzt und eine Pleite vor Ablauf der gewünschten 30 Jahre droht. Im besten Fall würde stattdessen heute eine Ralley des Aktienmarktes beginnen und das Depot würde schneller wachsen als die monatlichen Entnahmen.

Leider wissen wir natürlich nicht, wie sich der Aktienmarkt in den nächsten 30 Jahren entwickeln wird, sodass wir Annahmen treffen müssen. Prinzipiell gäbe es die folgenden Möglichkeiten, diesem Problem rechnerisch auf den Grund zu gehen:

• Wir rechnen mit einer gemittelten Rendite des Aktienmarktes. Historisch hat zumindest der amerikanische Aktienmarkt im Schnitt über 6% jährliche Rendite nach Abzug der Inflation geliefert. Diese 6% werden wohl viele in ihren eigenen Excel-Berechnungen zu dem Thema als Parameter verwenden. Problematisch ist hier, dass eine mittlere Rendite aber das sog. Rendite-Reihenfolge-Risiko (Im Englischen “Sequence-of-Return-Risk”) völlig außer Acht lässt. Bei regelmäßigen Entnahmen macht es nämlich einen substantiellen Unterscheid ob Einbrüche des Aktienmarktes früh in der Entnahmephase passieren oder erst später. Dies ist dann auch der Grund, warum so etwas wie die Trinity-Studie überhaupt notwendig war. Würde es dieses Risiko nicht geben, könnte man als Entnahme einfach genau die gemittelte Rendite nehmen und hätte dann somit eher eine “6%-Regel”.

• In diesem Simulator gehen wir daher einen anderen Weg: Es gibt ausgezeichnet gepflegte Daten zum amerikanischen Aktienmarkt und zur Inflation, die bis in das Jahr 1871 zurück reichen und von Robert Shiller monatlich aktualisiert werden. Dies ergibt 153*12=1836 monatliche Datensätze, die wir verwenden können um mögliche zukünftige Kursentwicklungen zu prognostizieren. Wir tun dies indem wir einen dieser historischen Datensätze nehmen, z.B. April 1962 und unser Aktiendepot so weiterentwickeln, als wären wir im April 1962 in den Ruhestand gegangen und hätten danach die Aktienmarktentwicklungen der 30 Jahre zwischen April 1962 und April 1992 exakt noch einmal durchlebt. Dies ergibt eine mögliche Historie, die isoliert betrachtet natürlich nicht viel aussagt. Wir können dies aber mit den verbleibenden 1835 “Historien” ebenfalls tun und erhalten dann ein großes Spektrum möglicher Entwicklungen unseres Depots. Immerhin passierten zwischen 1871 und heute, eine Weltwirtschaftskrise, zwei Weltkriege, eine Ölkrise, eine Dot-Com Blase und mehrere große und kleine Finanzkrisen. Grundannahme dieses Simulators ist, dass damit bereits ein sehr großes Spektrum an möglichen Extremsituationen abgedeckt ist und wir davon ausgehen, dass die tatsächliche zukünftige Entwicklung unseres Portfolios mit recht hoher Wahrscheinlichkeit irgendwo zwischen den Extremen liegen wird.

Die zeitlichen Entwicklungen des Depots können für alle Starthistorien “angefahren” werden

Diese möglichen Historien können wir nun in unserem Simulator genauer betrachten. Das rechte Diagramm im Simulator zeigt helblau hinterlegt den “Korridor” in dem sich alle historischen Depotentwicklungen bewegt haben, d.h. die untere hellblaue Grenze wurde in allen betrachteten Historien niemals unterschritten und die obere Grenze wurde historisch niemals überschritten. Der etwas dunkler eingefärbte Bereich wird durch das sogenannte erste und dritte Quantil begrenzt, d.h. in diesem Bereich befinden sich 50% der mittleren Entwicklungen. In dessen Mitte befindet sich schließlich der Median, d.h. der Mittelwert aller betrachteten historischen Entwicklungen.

Dunkelblau dargestellt ist im Standard immer die Depot-Entwicklung im schlimmsten möglichen Fall aller durchgerechneten Historien, welcher zum niedrigsten Endwert des Depots führt. Schauen wir uns diesen Fall einmal genauer an: Die Grafiken sind interaktiv, d.h. wir können mit der Maus den Anfang der Kurve markieren und vergrößern. Wir sehen dann, dass wir bereits in den ersten beiden Monaten nach Beginn unseres Ruhestands heftige Kurseinbrüche erleiden. Unser Depot sinkt erst um 11% und dann einen Monat später noch einmal um 27%. Wir erleben hier also quasi live den Alptraum jedes Privatiers. Um unsere monatlichen 1600€ durch Aktienverkäufe zu bestreiten müssen wir plötzlich deutlich mehr Anteile verkaufen und das Depot schmilzt daher so schnell ab, dass wir bereits im Februar 2039 pleite wären. Rein Rechnerisch hätten wir am Ende unseres Betrachtungszeitraums von 30 Jahren, also im Juli 2052, sogar noch Schulden bei unserer Depotbank in Höhe von 1.3 Mio. € da wir ja weiterhin monatlich 1.600€ für unsere Lebenshaltung entnehmen müssen. Wenn wir uns den Schieberegler ganz unten auf der Seite oder die Beschriftung der dunkelblauen Kurve im Diagramm selber ansehen, sehen wir welche der möglichen Historien hier als “Worst-Case” dargestellt wird. Die schlimmst mögliche Historie für unseren einfachen Beispielfall startet im September 1929 und der katastrophale Kurseinbruch der hier zuschlägt ist genau der Höhepunkt der Weltwirtschaftskrise im September und Oktober 1929.

Wenn wir jetzt auf den grünen Knopf “Springe zum Best-Case” drücken sieht das Bild natürlich komplett anders aus. Der Schieberegler unten springt dazu interessanterweise gar nicht weit, nämlich zum Juni 1932 als die Wirtschaft zur großen Erholung nach der Krise ansetzt. Die blaue Kurve, die die Depotentwicklung mit diesem virtuellen Startmonat zeigt, verläuft jetzt in der Nähe der oberen Grenze des Korridors und endet per Definition als “Best-Case” rechts am oberen Ende des Korridors. Würde unser 30 Jahreszeitraum in dieser besten aller Möglichkeiten starten, hätten wir am Ende ein Depotvermögen von 17.5 Mio. € angehäuft und unsere Erben würden sich die Hände reiben.

Diese beiden Extremfälle begrenzen sozusagen das Spektrum aller Möglichkeiten was unserem Depot in den 30 Jahren wiederfahren sollte. Natürlich kann niemand ausschließen, dass zukünftig noch extremere Szenarien kommen. Zumindest in den letzten 151 Jahren gab es aber keine extremeren Verläufe als diese. Der Schieberegeler unten erlaubt es uns jetzt auch virtuell durch alle möglichen anderen “Starthistorien” zu reisen und sich die zugehörigen Depotverläufe auf der rechten Grafik anzusehen. Wenn wir zurück zum Worst-Case wollen, reicht ein Druck auf den roten Knopf.

Hier sind beide Fälle noch einmal exemplarisch dargestellt. Links der Worst-Case, rechts der Best-Case:

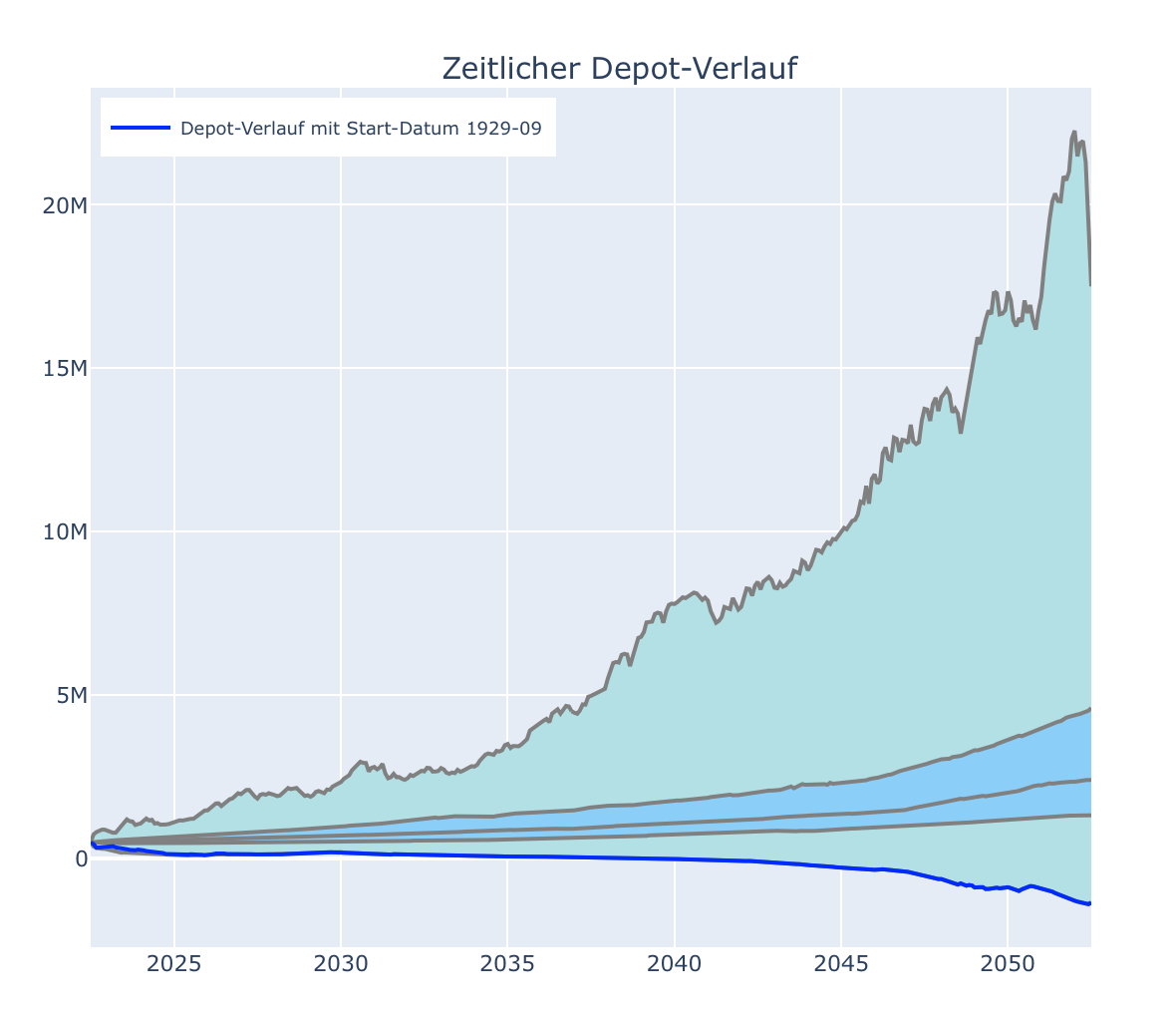
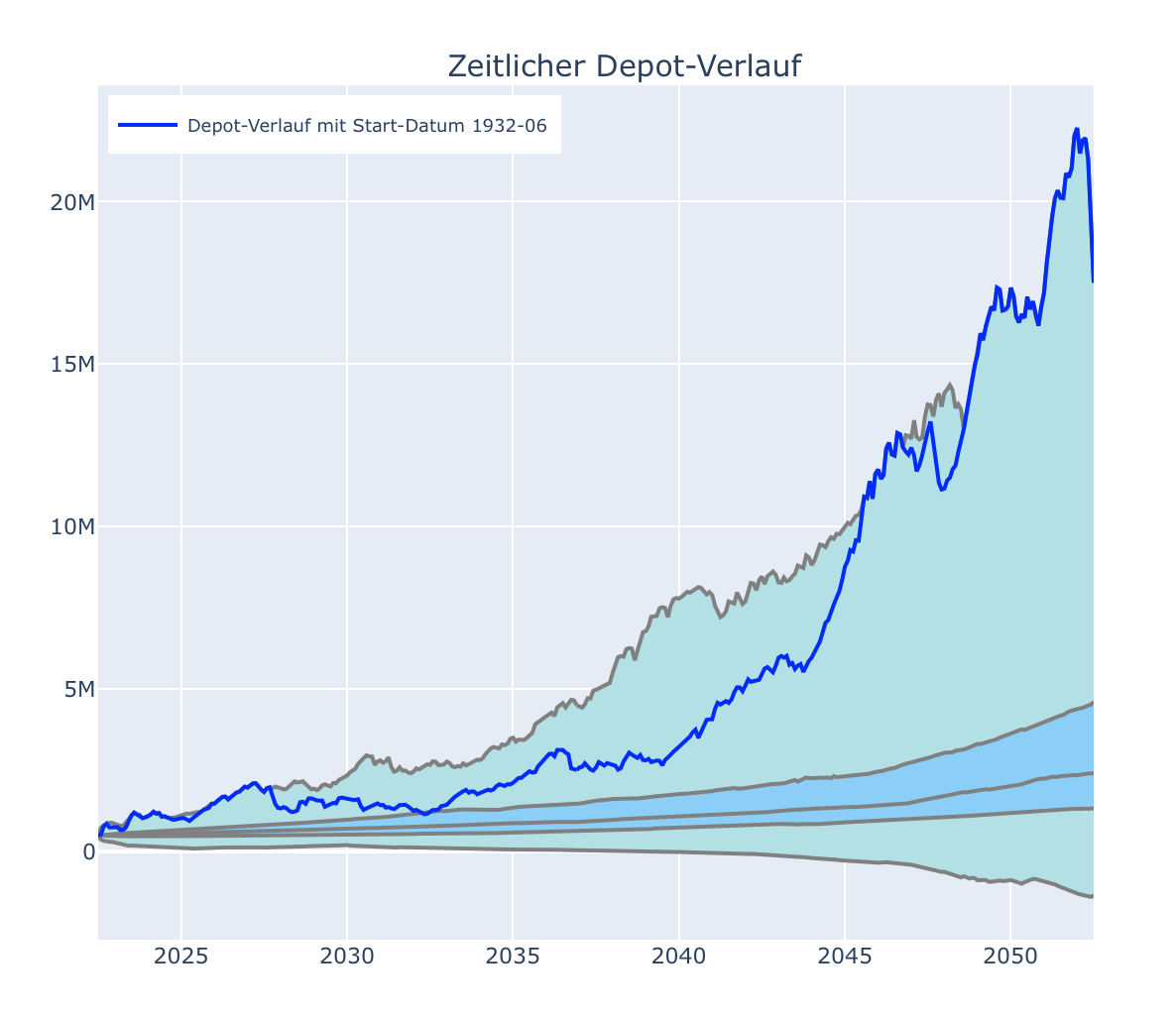
Wenn man sich den Bereich rechts unten genauer ansieht, stellt man aber fest, dass das Minimum der Entwicklungen bei strikter Anwendung der 4% Regel immer noch unterhalb der Nulllinie liegt. Dies bedeutet, dass die 4% Regel entgegen der landläufigen Meinung keinesfalls eine sichere Entnahme-Strategie ist. Trotzdem landet die übergroße Mehrzahl aller Möglichkeiten nach 30 Jahren im positiven Bereich und die Anwendung der 4%-Regel kann daher durchaus Sinn machen, wenn man sich der verbleibenden Risiken bewusst ist. Genau dafür soll dieser Simulator ja ein besseres Gefühl vermitteln, indem er ein großes historisches Spektrum aller Möglichkeiten zeigt.

Schauen wir jetzt, was passiert, wenn wir statt der 4% nur 3% jährlich entnehmen. Dies entspricht einer monatlichen Entnahme von 1.200€, die wir daher in das Feld “Ausgaben ab FI” eintragen. Der Simulator aktualisiert nach Eingabe sofort seine Daten neu für alle Historien und man sieht direkt, dass sich der gesamte Korridor deutlich nach oben bewegt hat. Schaut man sich den vergrößerten Bereich um das Minimum nahe beim Ende des Simulationszeitraums an, sieht man dies noch deutlicher, hier links mit 4% Entnahme und rechts mit 3%:

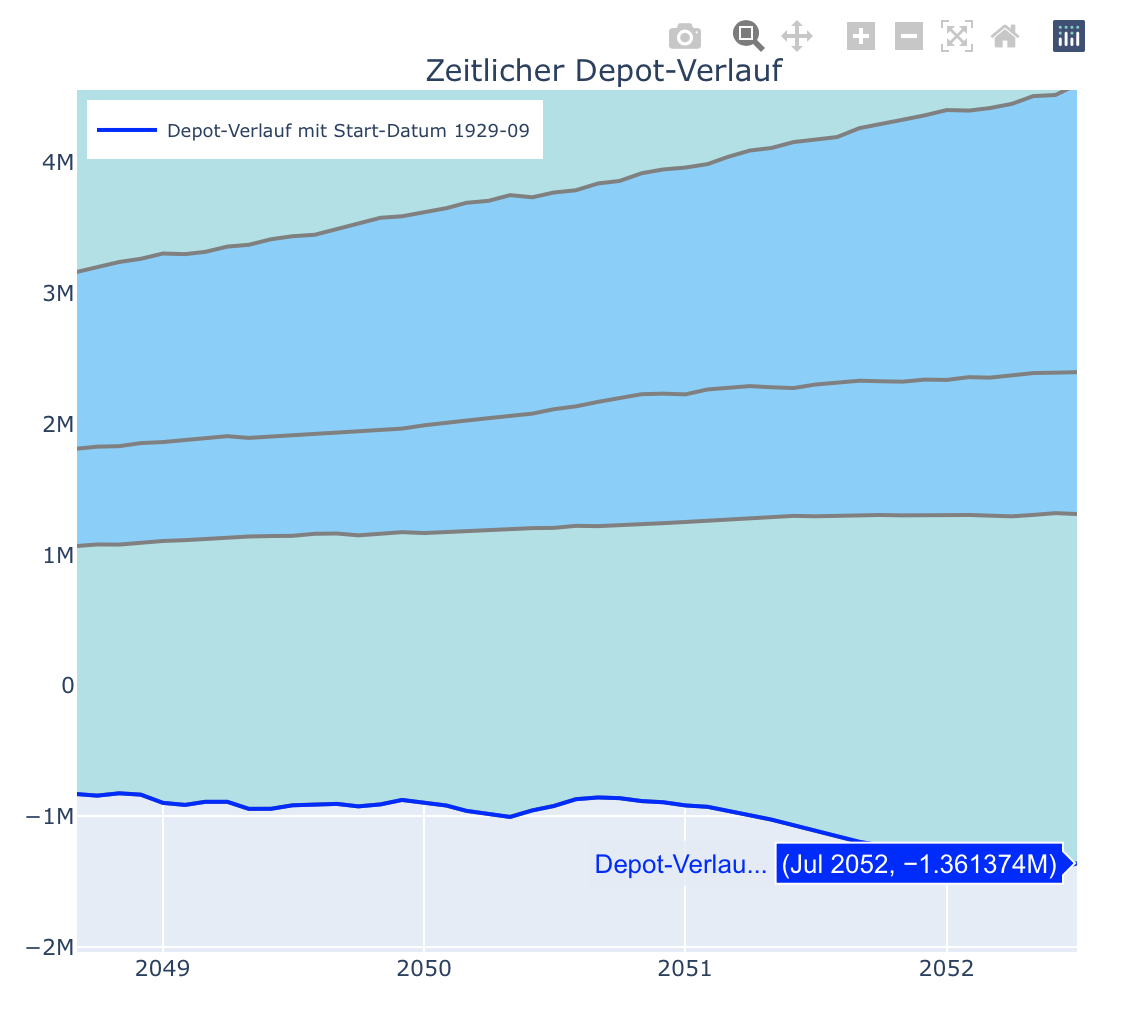
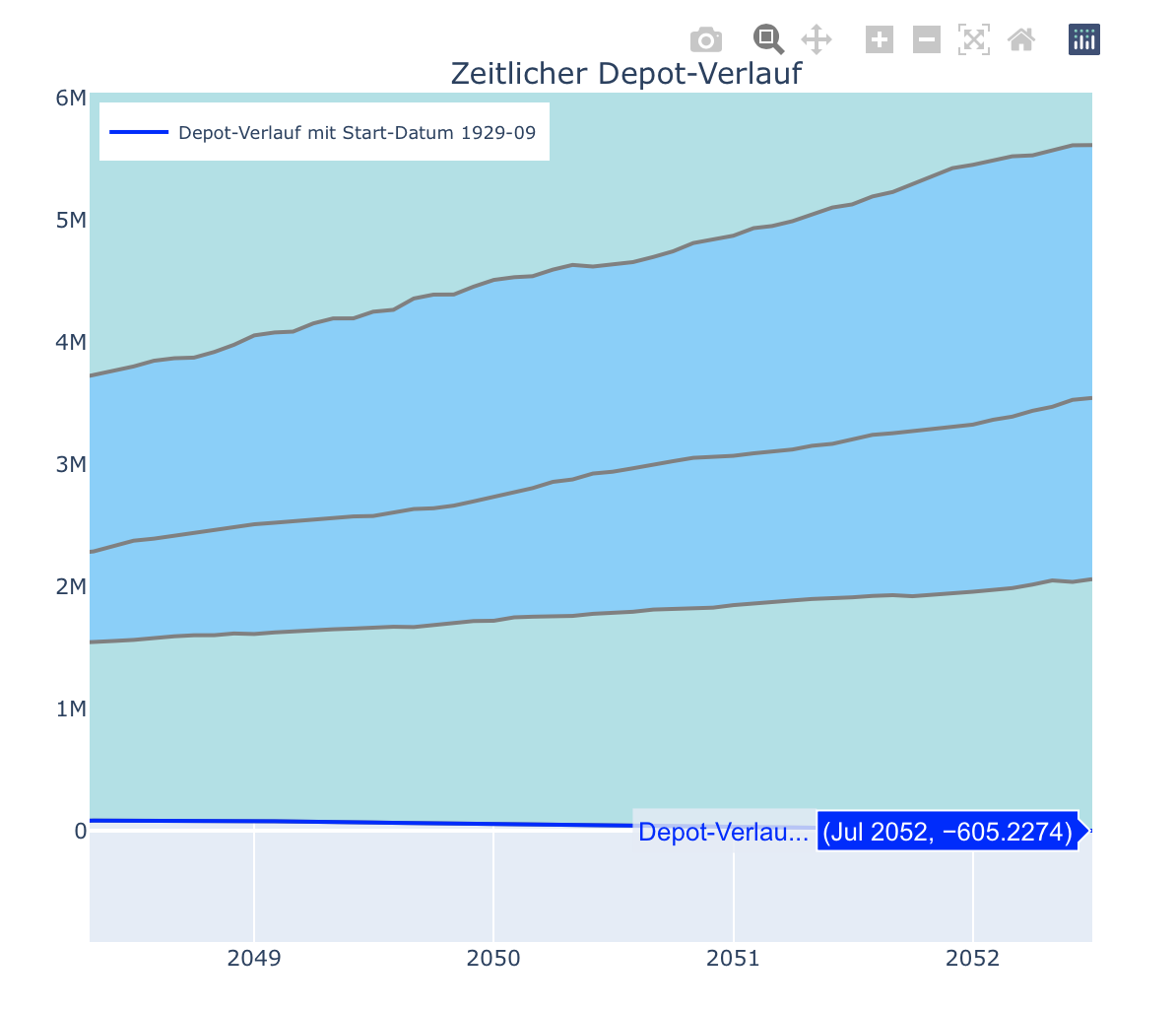
Das Minimum liegt jetzt fast genau auf der Null-Linie, d.h. es gibt kaum noch Historien, die nach 30 Jahren zu einer Pleite führen. Eine Entnahme von 3% erscheint somit deutlich sicherer als die Anwendung der 4%-Regel, zumindest wenn mann auch solche Extremereignisse, wie eine erneute Weltwirtschaftskrise abfedern möchte. Wir sehen an dieser Stelle bereits, dass wir die Ergebnisse der Trinity-Studie (für den hier angenommenen 100% Aktienanteil) mit dem Simulator sehr gut bestätigen können. Unser Simulator kann aber noch deutlich mehr.

Exakte Berechnung der Entnahmeraten

Dazu wechseln wir jetzt auf den zweiten Reiter des Simulators, der mit “Exakt berechnete Entnahmeraten” bezeichnet ist und genau dies tut. Wir nehmen an dieser Stelle keine Veränderungen der Einstellungen vor und erhalten dort die folgende Übersicht:

Die Tabelle (die übrigens per Knopfdruck auch als Excel-File exportierbar ist) zeigt nun exakt berechnete Entnahmeraten und zugehörige Pleite-Wahrscheinlichkeiten. Wenn wir unten beginnen sehen wir, dass eine monatliche Entnahmerate von exakt 1199,82€ dazu führt, dass wir eine Pleitewahrscheinlichkeit von 0% erhalten. Dies bedeutet

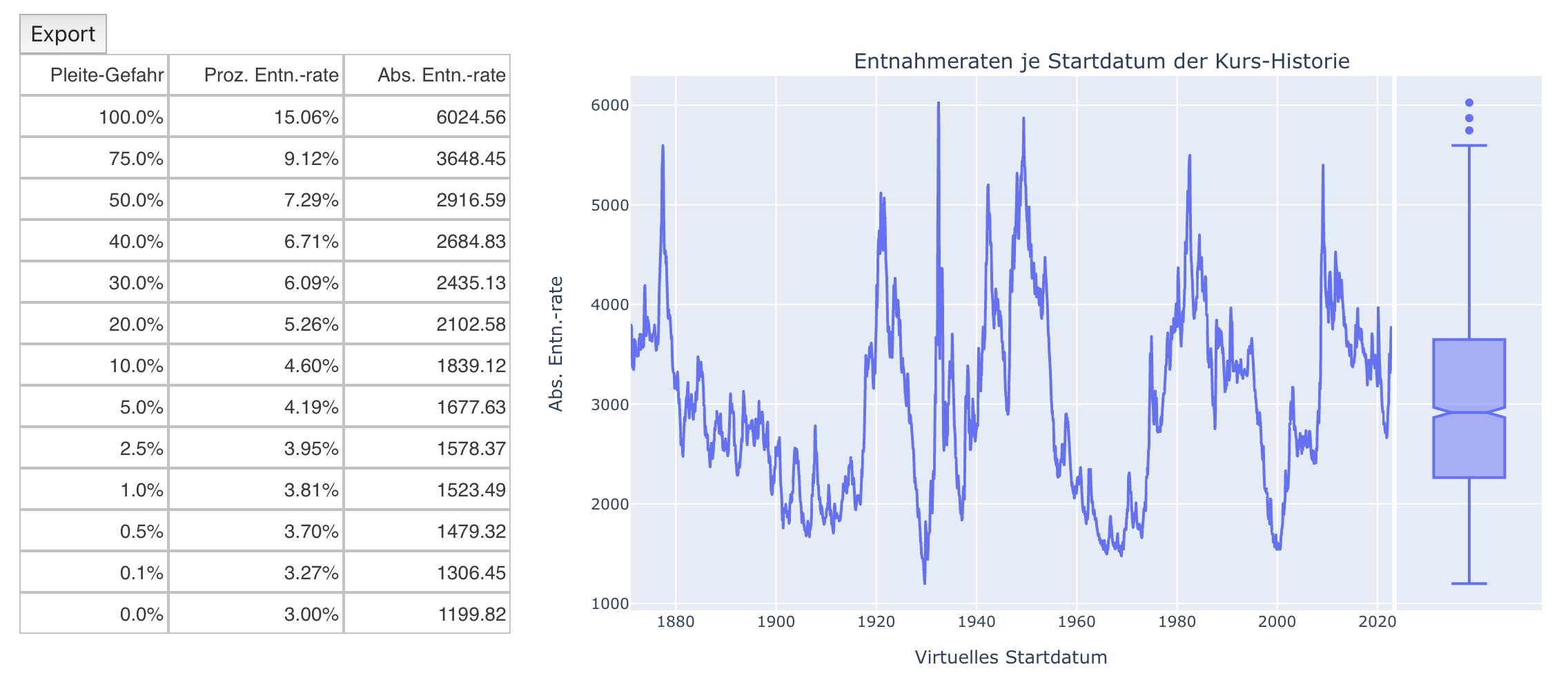
• Keine der möglichen Historien führt am Ende zu einem negativen Depot-Wert
• Das Minimum des Depot-Endwertes nach 30 Jahren ist für den Worst-Cast exakt 0.

Wer möchte, kann die 1200€ als “Ausgaben ab FI” wieder eintragen und sich die Historien, insb. für den Worst-Case und den Box-Plot einmal ansehen. Das Depot landet am Ende beim Worst-Case exakt bei 0.

Die hier rechts dargestellte Grafik zeigt jetzt die exakt berechneten Entnahmeraten für jeden virtuellen Startzeitpunkt der Kurs-Historie. Exakt berechnet bedeutet hier wiederum, dass die so gebildete Entnahmerate für jeden virtuellen Startpunkt am Simulationsende das Portfolio genau auf Null gesetzt hätte. Wir sehen dort, dass das Minimum der so berechneten Entnahmeraten dem schon bekannten virtuellen Startdatum im September 1929 entspricht, analog wie wir das auf dem ersten Reiter bereits gesehen hatten. Der Box-Plot ganz rechts fasst die Verteilung der so gebildeten Einnahmeraten noch einmal kompakt zusammen und ist eine analoge Darstellung zur Tabelle.

Aus der Tabelle erkennt man dann auch eine etwas bessere Interpretation der 4%-Regel: Wenn man sich die Zeile zur Pleite-Wahrscheinlichkeit von 2.5% ansieht, erhält man eine jährliche prozentuale Entnahmerate von 3,96%. Die 4%-Regel akzeptiert somit für einen 30 Jahre Zeithorizont eine Pleite-Wahrscheinlichkeit von ca. 2.5%. Dies kann dennoch ein vernünftiger Startpunkt für eigene Überlegungen sein, insb. wenn man außer den geplanen Depot-Entnahmen auch noch andere Einkünfte hat. Dies ist aber ein Thema für einen anderen Artikel. Dort gehe ich dann auch detailliert auf die Einahme- / Ausgabegrafik des ersten Reiters ein, die ich in dieser konzeptionellen Einführung zunächst komplett ignoriert habe.